Instrumentation & Automation
Windows ⁄ Android ⁄ macOS ⁄ iOS
In electrical engineering, sometimes it is necessary to calculate the parameters of a conductor depending on the substance from which it is made, resistance, cross-section, length and temperature. An unit is built into the Instrumentation & Automation application that allows you to calculate:
- The resistance of an electrical conductor in terms of its length, cross-section, temperature and the substance from which it is made.
- The length of the electrical conductor according to its cross-section, temperature and substance from which it is made.
- Cross-section of an electrical conductor for a given current ⁄ power.
Electrical conductor
Calculation of parameters
The electrical properties of a conductor are highly dependent on the material from which it is made. The most important are:
- Specific resistance of the conductor substance [ρ], measured in Ohm·m in the international system of units (SI). This means that the SI unit of resistivity is the resistivity of a substance such that a homogeneous conductor 1 m long with a cross-sectional area of 1 m², made of this substance, has a resistance of 1 Ohm.
Also, the off-system unit Ohm·mm²/m is often used.
1 Ohm·mm²/m = 10−6 Ohm·m
- The temperature coefficient of electrical resistance [α] characterizes the dependence of electrical resistance on temperature and is measured in Kelvin minus the first power K−1. This is a value equal to the relative change in the specific ⁄ electrical resistance of a substance with a change in temperature by one unit. The calculation of the resistivity ρt at an arbitrary temperature t is performed according to the classical formula (1):
ρt = ρ20[1 + α(t - 20)]
ρt - specific resistance at temperature t
t - temperature
ρ20 - specific resistance at 20 ° C
α - temperature coefficient of resistance
The formula is applicable in a small temperature range: from 0 to 100 ° C. Outside this range, or for accurate results, more complex calculations are used.
Below is a table of the most popular metals for the manufacture of conductors, with their resistivity and temperature coefficients of electrical resistance. The data are taken from various sources. It should be noted that both the specific resistance of the conductor and its temperature coefficient of electrical resistance depend on the purity of the metal, and in the case of alloys (steel), they can differ significantly from brand to brand.
| Table 1 |
| Metal | Specific resistance [ρ]
at t = 20 °C, Ohm·mm²/m | Temperature coefficient of electrical resistance
[α], K−1 |
| Copper | 0.0175 | 0.0043 |
| Aluminum | 0.0271 | 0.0039 |
| Steel | 0.125 | 0.006 |
| Silver | 0.016 | 0.0041 |
| Gold | 0.023 | 0.004 |
| Platinum | 0.107 | 0.0039 |
| Magnesium | 0.044 | 0.0039 |
| Zinc | 0.059 | 0.0042 |
| Tin | 0.12 | 0.0044 |
| Tungsten | 0.055 | 0.005 |
| Nickel | 0.087 | 0.0065 |
| Nickeline | 0.42 | 0.0001 |
| Nichrome | 1.1 | 0.0001 |
| Fechral | 1.25 | 0.0002 |
| Chromal | 1.4 | 0.0001 |
When calculating the properties of an electrical conductor, the Instrumentation & Automation application operates with the following input ⁄ output parameters and their units of measurement:
- Substance from which the conductor is made (See table 1)
- Conductor length. mm, cm, m, km, inches, feet, yards
- Conductor temperature. ° C, ° F
- Conductor diameter. mm
- Conductor cross section. mm², kcmil
kcmil - thousand circular mils = 0.5067 mm²
- Conductor resistance. Ohm, kOhm, MOhm
Below, the figures show screenshots of the Instrumentation & Automation application modules for calculating the conductor parameters.
Calculation of the resistance of an electrical conductor
We calculate the resistance of an electrical conductor using the formula:
R = ρ * L / S
- R is the resistance of the electrical conductor
- ρ is the specific resistance
calculated by the formula (1): ρ = ρ20[1 + α(t - 20)]
- ρ20 is the specific resistance of the conductor at a temperature of t = 20 ° C (Table 1)
- t is the conductor temperature
- α is the temperature coefficient of electrical resistance (Table 1)
- L is the length of the electrical conductor
- S is the cross-section of electrical conductor
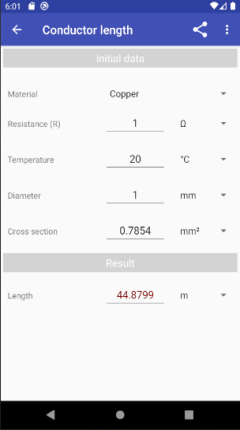
Calculating the length of an electrical conductor
We calculate the length of the electrical conductor using the formula:
L = R * S / ρ
- L is the length of the electrical conductor
- R is the resistance of the electrical conductor
- S is the cross-section of electrical conductor
- ρ is the specific resistance
calculated by the formula (1): ρ = ρ20[1 + α(t - 20)]
- ρ20 is the specific resistance of the conductor at a temperature of t = 20 ° C (Table 1)
- t is the conductor temperature
- α is the temperature coefficient of electrical resistance (Table 1)
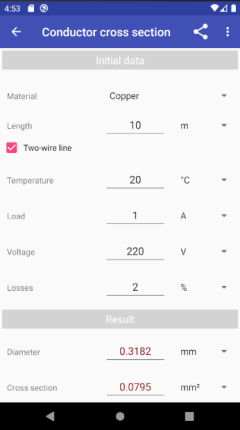
Calculation of the cross-section of an electrical conductor
The minimum cross-section of an electrical conductor with allowable voltage losses is calculated by the formula:
S = I * ρ * L / ΔU
- S is cross-section of electrical conductor
- I is current in the electric circuit
- L is the length of the electrical conductor
with a two-wire line, the conductor length (L value) is doubled
- ΔU is allowable voltage loss
- ρ is the specific resistance
calculated by the formula (1): ρ = ρ20[1 + α(t - 20)]
- ρ20 is the specific resistance of the conductor at a temperature of t = 20 ° C (Table 1)
- t is the conductor temperature
- α is the temperature coefficient of electrical resistance (Table 1)