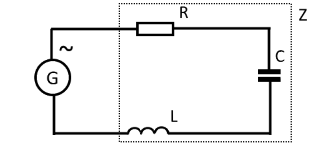
Series connection R, L, C
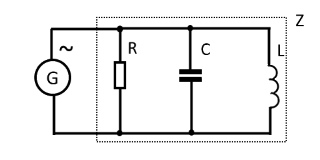
Parallel connection of R, L, C
In the Android Instrumentation & Automation application, in the section "Electrics" a unit for calculating Ohm's law for direct and alternating current is included. First a bit of theory ..
Ohm's law determines the relationship between the current (I), the voltage (U) and the resistance (R) in the electrical circuit. The most common concept is:
The current in the circuit is directly proportional to the voltage and inversely proportional to the electrical resistance of the circuit, i.e.
| I = U / R | where | I - Amperage, measured in Amperes, (A) |
| U - the voltage measured in Volts, (V) | ||
| R - resistance, measured in Ohms, (Ω) |
Ohm's law is fundamental in electrical engineering and electronics. Without its understanding, the job of a specialist in the field of instrumentation and automation is not possible.
In addition to Ohm's law, the most important is the concept of electrical power, P:
The power of direct current (P) is equal to the product of the current (I) by the voltage (U), i.e.
| P = I × U | where | P is the electrical power measured in watts, (W) |
| I - Amperage, measured in Amperes, (A) | ||
| U is the voltage measured in Volts, (V) |
Combining these two formulas, we derive the relationship between the amperage, voltage, resistance and power, and create the following table:
| Amperage | I= | U/R | P/U | √(P/R) |
| Voltage | U= | I×R | P/I | √(P×R) |
| Resistance | R= | U/I | P/I² | U²/P |
| Electrical power | P= | I×U | I²×R | U²/R |
A practical example of using table formulas: Buying an iron in the store, with a power of 1 kW (1 kW = 1000 W), calculate the minimum current for the socket to withstand into which this purchase is intended:
Despite the fact that the iron uses AC, we neglect its reactance (see below), and use the simplified formula for direct current. We find in the table I = P / U. We get: 1000 kW / 220 V = 4.5 Ampere. This is the minimum current that the socket must withstand when a load of 1 kW is connected to it.
The most common multiplier prefixes:
In an alternating current circuit, Ohm's law can have some of the features described below.
In the alternating current circuit, the resistance except the active (R) can have both capacitive (C) and inductive (L) components. In this case, the concept of electrical impedance, Z (full or complex resistance for a sinusoidal signal) is introduced. Simplified circuits of complex resistance are shown in the figures below, on the left for the serial, on the right for parallel connection of the inductive and capacitive components.
Also, the impedance Z, depends not only on the capacitive (C), inductive (L) and active (R) components, but also on the frequency of the alternating current.
| Impedance, Z | |
| R, L, C are sequentially connected | R, L, C are parallely connected |
| Z=√(R2+(ωL-1/ωC)2) | Z=1/ √(1/R2+(1/ωL-ωC)2) |
| where, | |
| ω = 2πγ - cyclic angular frequency; γ - the frequency of the alternating current | |
The power factor is the ratio of the active power (P) of the consumer of electrical energy to the total (S) power consumption, i.e.
Cos(φ) = P / S
It also shows how the alternating current flowing through the load relative to the voltage applied to it is shifted in phase.
Changes from 0 to 1. If the load does not contain reactive components (capacitive and inductive), the power factor is equal to one.
The closer Cos (φ) to one, the less energy loss in the electrical circuit.
Based on the above concepts of the impedance Z and the power factor Cos (φ) characteristic of alternating current, we derive the formula for Ohm's law, power factor and their derivatives for alternating current circuits:
| I = U / Z | where | I - Amperage, measured in Amperes, (A) |
| U - the voltage measured in Volts, (V) | ||
| Z - impedance, measured in Ohms, (Ω) |
Derivatives of the formula:
| Amperage | I= | U/Z | P/(U×Cos(φ)) | √(P/Z) |
| Voltage | U= | I×Z | P/(I×Cos(φ)) | √(P×Z) |
| Impedance | Z= | U/I | P/I² | U²/P |
| Electrical power | P= | I²×Z | I×U×Cos(φ) | U²/Z |
The Android Instrumentation & Automation application includes a unit for calculating Ohm's law for both direct and alternating current, and for calculating impedance and power factor Cos (φ). Screenshots are presented in the pictures below: