In practical calculations of specialists in industrial automation, as well as in the design of automated control systems for technological processes, it is often required to calculate the surface area, and the volume of various geometric shapes.
These calculations are implemented in the Android application "Instrumentation & Automation". Below are the formulas by which the program calculates the area and volume of geometric shapes.
Table 1.
| Calculating the lengths and areas of plane figures |
| S - area | n - number of sides of a regular polygon |
| p - semiperimeter | r - radius of inscribed circle |
| P - perimeter | R - radius of the circumscribed circle |
| h - height | α - angle in radians |
| C - circumference | β - angle in degrees |
| l - arc length | |
| Triangle |
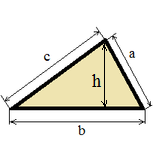 |
S = (b h) / 2;
S = (a b c) / (4 R);
S = p r;
S = √(p(p-a)(p-b)(p-c));
p = (a + b + c) / 2; |
| Parallelogram |
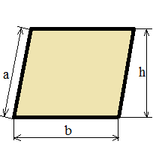 |
S = b h; |
| Rhombus |
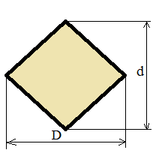 |
S = (D d) / 2; |
| Rectangle |
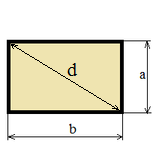 |
S = a b;
S = a√(d2 - a2);
S = b√(d2 - b2);
d = √(a2 + b2); |
| Trapezium |
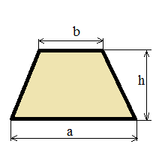 |
S = ((a + b) / 2) h; |
| Regular polygon |
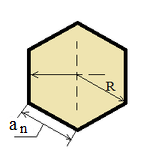 |
Sn = (n an r) / 2;
Sn = ((n an) / 2) √(R2 - (r2 / 4));
Pn = 2 n R Sin(π / n); |
| Circle |
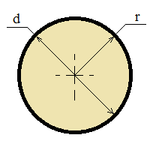 |
S = π r2;
S = (π d2) / 4;
C = 2 π r;
C = π d; |
| Sector |
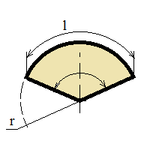 |
l = α r;
S = (r2 α) / 2;
l = (π r β) / 180;
S = (π r2 β) / 360; |
| Segment |
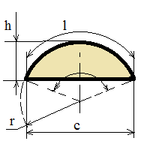 |
c = 2 √(h (2 r - h));
S = ½ (r l - c (r - h)); |
| Ring |
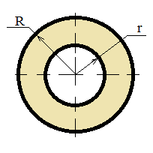 |
S = π (R2 - r2); |
| Ring sector |
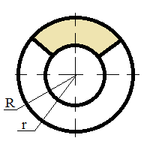 |
S = α (R2 - r2) / 2;
S = β π (R2 - r2) / 360; |
| Ellipse |
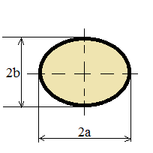 |
S = π a b; |
| Calculation of areas of surfaces and volumes of geometric bodies |
| S - surface area | r - radius of a circle |
| Ssid - side surface area | R - ball radius |
| Sbs - base area | D - ball diameter |
| Pbs - base perimeter | H - height |
| V - volume | a - apothem |
| l - generatrix |
| Rectangular parallelepiped |
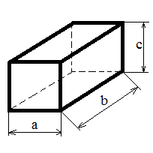 |
S = 2 (ab + bc + ac);
V = a b c; |
| Cube |
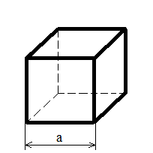 |
S = 6 a2;
V = a3; |
| Regular pyramid |
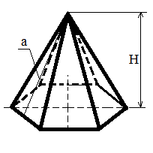 |
Ssid = ½ Pbs a;
V = (Sbs H) / 3; |
| Regular truncated pyramid |
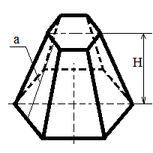 |
Ssid = ½ (Pbs1 + Pbs2) a;
V = H (Sbs1+Sbs2 + √(Sbs1Sbs2)) / 3; |
| Cylinder |
 |
Ssid = 2 π r H;
S = 2 π r H + 2 π r2;
V = π r2 H; |
| Hollow cylinder |
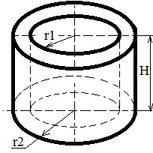 |
Ssid = 2 π H (r1 + r2);
V = π H (r22 - r12),
r2 > r1; |
| Cone |
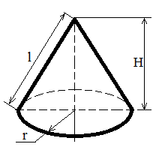 |
Ssid = π r l;
Ssid = π r √(r2 + H2);
V = (π r2 H) / 3; |
| Truncated cone |
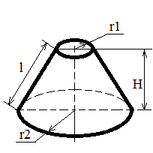 |
Ssid = π l (r1 + r2);
V = π H (r12 + r22 + r1 r2) / 3; |
| Ball |
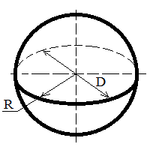 |
S = 4 π R2;
S = π D2;
V = 4 π R3 / 3;
V = π D3 / 6; |
| Ball sector |
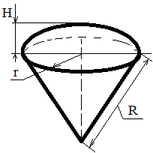 |
Ssid = π R (r + 2H);
V = (2 π R2 H) / 3; |
| Ball segment |
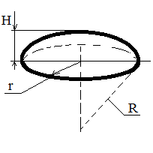 |
Ssid = 2 π R H;
V = (π H (3 r2 + H2)) / 6;
V = (π H2 (3 R - H)) / 3; |






















