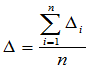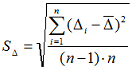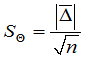Errors. Classes of accuracy of measuring instruments.

Let me first take a little digression. Such concepts as error, accuracy class are described in detail in the regulatory documentation GOST 8.009-84 «Standardized metrological characteristics of measuring instruments», GOST 8.401-80 «Classes of accuracy of measuring instruments. General requirements» and the like. But opening those documents at once a feeling of melancholy .. So dry and incomprehensible to the beginning «specialist», these concepts are explained. Let us now discard such pretentious and incomprehensible definitions as «the mean square deviation of the random component of the error» or «normalized autocorrelation function» or «the characteristic of the random component of the error from the hysteresis - the variation H of the output signal (indication) of the measuring instrument», and so on. Let's try to understand, and then reduce to one concept, what exactly is «accuracy» and what types it happens.

Measurement errors – deviation of the measurement results from the true value of the measured value. Errors are inevitable, it is impossible to reveal the true value.

Measurement errors are subdivided:

1. Absolute error: Δ = X_r - X_m is expressed in units of the measured value, for example, in kilograms (kg), when measuring the mass.
   where X_r is the actual value of the measured quantity, usually the reference value;
   X_m is the measured value.
2. Relative error: δ = (Δ ⁄ X_r) · 100, is expressed in % of the actual value of the measured value.
3. Reduced error: γ = (Δ ⁄ X_n) · 100, is expressed in % of the normalizing value.
   where X_n is the normalizing value expressed in the same units as Δ, usually the measuring range of the instrument (scale).

By the nature of manifestation:

• systematic (may be excluded from the results);
• random;
• rough or slips (usually not included in the measurements).

Depending on the operation of the devices:

• the main is the error of the measuring instrument under normal conditions; (GOST 8.395-80)
• the additional error is a component of the error of the measuring instrument, which in addition arises due to the deviation of any of the influencing values from the normative value or the output beyond the normal range of values. For example: measurement of excess pressure under operating conditions, at an ambient temperature of 40 °C, a relative humidity of 18% and an atmospheric pressure of 735 mm Hg. which does not correspond to the nominal values of the influencing quantities during the calibration.

Name of error	Formula	Form of expression	Accuracy class designation
			Documentation	Device
Absolute	Δ = Xr - Xm	Δ = ±50 мг Examples: Nominal weight of weights 1 kg ± 50 mg Measuring range of weights of the middle class of accuracy from 20 g to 15 kg ± 10 g	Accuracy class: M1 Accuracy class: medium III Note: many types of measurements have their own regulatory documentation on the expression of errors, here, for example, is taken for weights.	М1
Relative	δ = (Δ ⁄ Xr) · 100	δ = ±0,5 Example: Measured value of excess pressure with relative error 1 bar ±0,5% ie. 1 bar ± 5 mbar (absolute error)	Accuracy class 0,5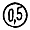
Reduced: the uniform scale	γ = (Δ ⁄ Xn) · 100	γ = ±0,5 Example: The measured value at the sensor overpressure, with a scale from 0 to 10 bar 1 bar (= 0.5% of 10 bar) 1 bar ± 50 mbar (absolute error)	Accuracy class 0,5	0,5
substantially uneven scale		γ = ±0,5 It is determined in the normative documentation for the device for each measurement range (scale) its normalizing value	Accuracy class 0,5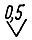

How to determine the error of the set of devices, which includes a primary device (sensor), a secondary converter (amplifier) and a secondary device. Each of the elements of this set has its own absolute, relative or reduced error. And in order to estimate the overall measurement error, it is necessary to bring all errors to one kind, and then calculate by the formula:

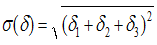
Further it will be interesting, probably, only to metrologists and that, only beginning. Now, let us recall a little about the mean square deviations (MSD). What are they needed for? Since the true value can not be revealed, it is necessary to at least most accurately approach it or determine a confidence interval in which the true value is with a high degree of probability. To do this, apply various statistical methods, we give the most common formulas. For example, you have performed n number of dimensions of anything and you need to define a confidence interval:

1. Determine the average arithmetic deviation:
   
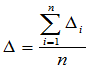
   n is the number of deviations
2. Define the mean square deviation (MSD) of the arithmetic mean:
   
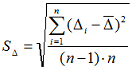
3. Calculate the random component of the error:
   
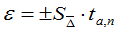
   t is the Student's coefficient, depending on the number of degrees of freedom
   Table 1.

   α =0,68		α =0,95		α =0,99
   n	tα,n	n	tα,n	n	tα,n
   2	2,0	2	12,7	2	63,7
   3	1,3	3	4,3	3	9,9
   4	1,3	4	3,2	4	5,8
   5	1,2	5	2,8	5	4,6
   6	1,2	6	2,6	6	4,0
   7	1,1	7	2,4	7	3,7
   8	1,1	8	2,4	8	3,5
   9	1,1	9	2,3	9	3,4
   10	1,1	10	2,3	10	3,3
   15	1,1	15	2,1	15	3,0
   20	1,1	20	2,1	20	2,9
   30	1,1	30	2,0	30	2,8
   100	1,0	100	2,0	100	2,6

4. Define the MSD systematic component of the error:
   
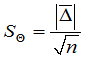
5. We calculate the total MSD:
   
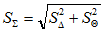
6. We determine the coefficient, which depends on the ratio of the random and systematic components of the error:
   
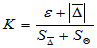
7. We estimate the confidence limits of error:
   

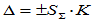
In recent times, the term «uncertainty» is increasingly heard. To my opinion, «expanded uncertainty of measurements» = basic error + additional, which takes into account all the influencing factors.