В практических расчетах КИП и А, а также при проектировании автоматизированных систем управления технологическими процессами нередко требуется расчет площади поверхности, и объема геометрических фигур - бак, цистерна и т.д.
В таблице 1 приведены наиболее употребительные формулы для расчета площади, объема и периметра.
Таблица 1.
| Вычисление длин и площадей плоских фигур |
| S - площадь | n - число сторон правильного многоугольника |
| p - полупериметр | r - радиус вписанной окружности |
| P - периметр | R - радиус описанной окружности |
| h - высота | α - величина угла в радианах |
| C - длина окружности | β - величина угла в градусах |
| l - длина дуги | |
| Треугольник |
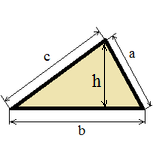 |
S = (b h) / 2;
S = (a b c) / (4 R);
S = p r;
S = √(p(p-a)(p-b)(p-c));
p = (a + b + c) / 2; |
| Параллелограмм |
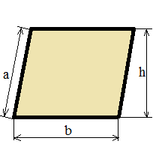 |
S = b h; |
| Ромб |
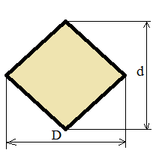 |
S = (D d) / 2; |
| Прямоугольник |
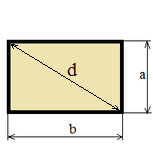 |
S = a b;
S = a√(d2 - a2);
S = b√(d2 - b2);
d = √(a2 + b2); |
| Трапеция |
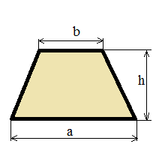 |
S = ((a + b) / 2) h; |
| Правильный многоугольник |
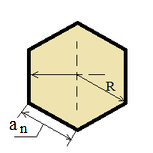 |
Sn = (n an r) / 2;
Sn = ((n an) / 2) √(R2 - (r2 / 4));
Pn = 2 n R Sin(π / n); |
| Круг |
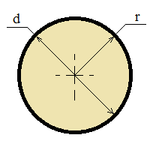 |
S = π r2;
S = (π d2) / 4;
C = 2 π r;
C = π d; |
| Сектор |
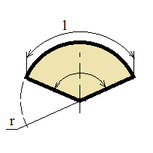 |
l = α r;
S = (r2 α) / 2;
l = (π r β) / 180;
S = (π r2 β) / 360; |
| Сегмент |
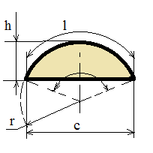 |
c = 2 √(h (2 r - h));
S = ½ (r l - c (r - h)); |
| Кольцо |
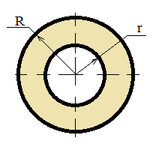 |
S = π (R2 - r2); |
| Кольцевой сектор |
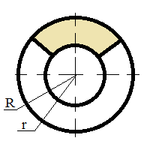 |
S = α (R2 - r2) / 2;
S = β π (R2 - r2) / 360; |
| Эллипс |
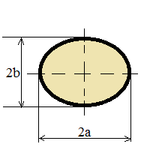 |
S = π a b; |
| Вычисление площадей поверхностей и объемов геометрических тел |
| S - площадь поверхности | r - радиус окружности |
| Sбок - площадь боковой поверхности | R - радиус шара |
| Sосн - площадь основания | D - диаметр шара |
| Pосн - периметр основания | H - высота |
| V - объем | a - апофема |
| l - образующая |
| Прямоугольный параллелепипед |
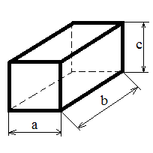 |
S = 2 (ab + bc + ac);
V = a b c; |
| Куб |
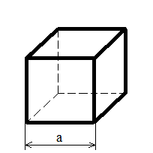 |
S = 6 a2;
V = a3; |
| Правильная пирамида |
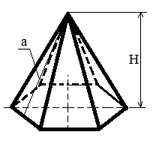 |
Sбок = ½ Pосн a;
V = (Sосн H) / 3; |
| Правильная усеченная пирамида |
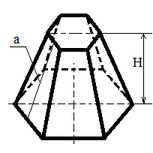 |
Sбок = ½ (Pосн1 + Pосн2) a;
V = H (Sосн1+Sосн2 + √(Sосн1Sосн2)) / 3; |
| Цилиндр |
 |
Sбок = 2 π r H;
S = 2 π r H + 2 π r2;
V = π r2 H; |
| Полый цилиндр |
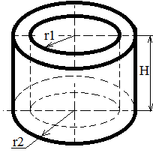 |
Sбок = 2 π H (r1 + r2);
V = π H (r22 - r12),
r2 > r1; |
| Конус |
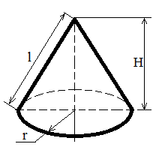 |
Sбок = π r l;
Sбок = π r √(r2 + H2);
V = (π r2 H) / 3; |
| Усеченный конус |
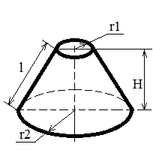 |
Sбок = π l (r1 + r2);
V = π H (r12 + r22 + r1 r2) / 3; |
| Шар |
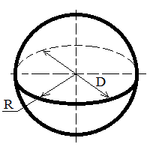 |
S = 4 π R2;
S = π D2;
V = 4 π R3 / 3;
V = π D3 / 6; |
| Шаровой сектор |
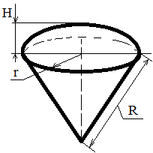 |
Sбок = π R (r + 2H);
V = (2 π R2 H) / 3; |
| Шаровой сегмент |
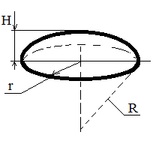 |
Sбок = 2 π R H;
V = (π H (3 r2 + H2)) / 6;
V = (π H2 (3 R - H)) / 3; |






















